Bridging Autoregressive and Diffusion Models for Robust Sequence Generation
Exploring a novel framework that unites autoregressive and diffusion-based approaches with hyperschedules, hybrid noising, and an adaptive correction sampler for superior sequence generation.
Introduction
Recent advances in sequence generation have largely focused on two dominant paradigms: the efficiency of autoregressive (AR) models (e.g., GPT [1]) and the robust, iterative refinement of diffusion-based models [2]. However, each approach has its limitations—AR models propagate errors without revision, while diffusion models, despite their error-correcting capabilities, suffer from slower inference. In this post, we present our unified framework that combines the strengths of both paradigms through innovative techniques such as hyperschedules, hybrid noising, and an Adaptive Correction Sampler (ACS). By incorporating additional insights from our full paper and the corresponding appendix, we aim to deliver a comprehensive guide that takes roughly 15 minutes to read.
Background & Motivation
Autoregressive models (e.g., GPT [1]) generate text one token at a time, offering low latency but with the inherent risk of cumulative errors. Diffusion models, in contrast, iteratively refine noisy inputs to correct errors—albeit at a higher computational cost [2]. Our work bridges these two strategies, allowing for dynamic correction mechanisms and improved overall generation efficiency. This unification not only mitigates the shortcomings of each paradigm but also opens up new avenues for practical applications.
The Unified Framework
Our approach introduces a continuum between traditional autoregressive decoding and iterative diffusion through:
- Hyperschedules: Customized noise schedules that vary per token, providing a smooth transition between AR and diffusion modalities.
- Hybrid Noising Processes: A blend of masking and random perturbations to train models in recognizing and correcting errors.
- Adaptive Correction Sampler (ACS): A novel inference algorithm that revisits and refines token decisions, thereby reducing the risk of error propagation.
Hyperschedules
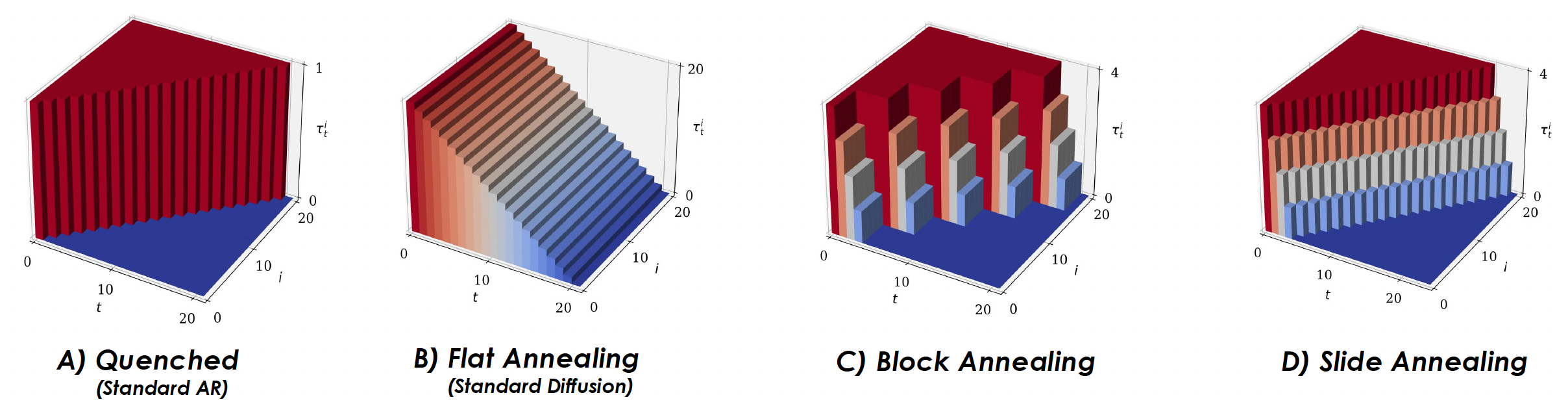
Standard diffusion models apply a uniform noise level across tokens. In our approach, hyperschedules assign a unique schedule to each token position, enabling a balance between the rigid structure of AR generation and the adaptability of diffusion. Our experiments (see Figure 1) highlight various designs—including “Quenched AR,” “Flat,” “Block,” and “Slide Annealing”—each with its own trade-offs in performance and efficiency.
Hybrid Noising Processes
To harness the benefits of both masking and randomness, we introduce a hybrid noising process:
- Absorbing Process: Gradually replaces tokens with a dedicated MASK token.
- Uniform Process: Randomly substitutes tokens with alternative tokens.
We explore two variants:
- γ-Hybrid: An approach based on an analytical framework inspired by SEDD [3].
- ε-Hybrid: A formulation utilizing weighted cross-entropy similar to MDM frameworks [4].
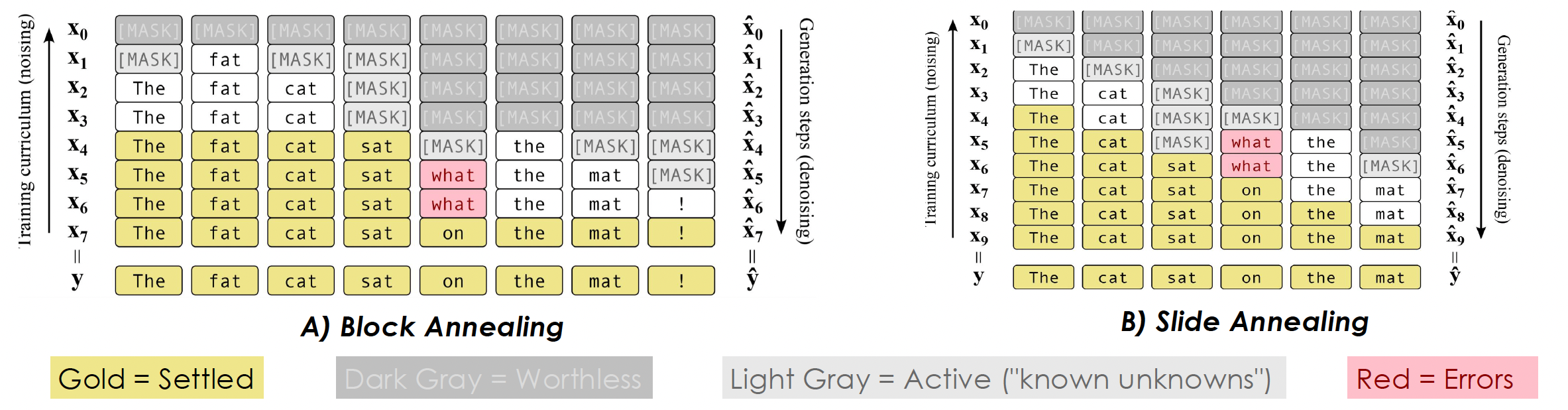
This combined strategy (illustrated in Figure 2) trains the model to progressively correct its own errors during sequence generation.
Adaptive Correction Sampler (ACS)
Traditional AR models do not allow revisiting earlier decisions. Our Adaptive Correction Sampler (ACS) breaks this limitation by iteratively refining token outputs. ACS leverages model confidence to adjust past predictions, ensuring minor mistakes do not cascade into major errors over the entire sequence. This iterative sampling is particularly valuable for generating longer and more coherent sequences.
Experimental Evaluation
We evaluated our unified models on benchmarks including WikiText, Lambada, Pubmed, and ArXiv. The key experimental findings are:
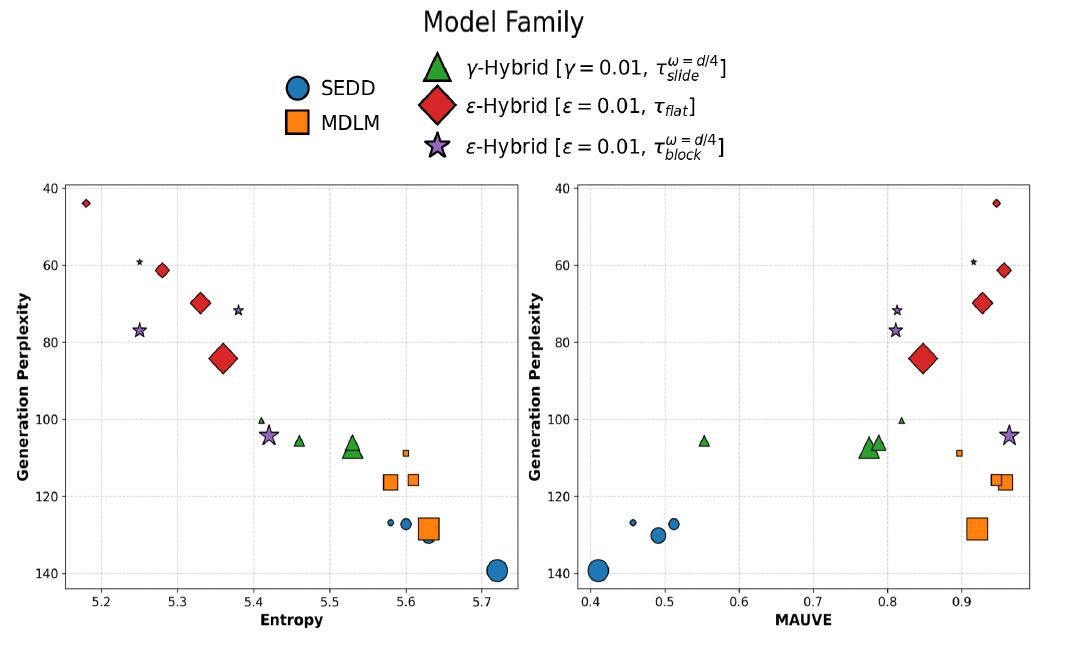
- Enhanced Generation Quality: Both γ-Hybrid and ε-Hybrid configurations show significantly improved perplexity and MAUVE scores (refer to Figure 3).
- Improved Trade-offs: Our model achieves superior quality-diversity trade-offs compared to baseline approaches, as quantified in the performance table below [3–5].
| Method | WikiText | Lambada | Pubmed | Arxiv |
|---|---|---|---|---|
| Transformer (Sahoo et al.) | 25.8 | 51.3 | 49.0 | 41.7 |
| SEDD (Lou et al.) | 36.0 | 48.9 | 45.4 | 40.0 |
| MDLM (Sahoo et al.) | 33.2 | 48.3 | 43.1 | 37.9 |
| BD3-LM (Arriola et al.) | 31.3 | 50.0 | 42.5 | 39.2 |
| γ-Hybrid (Ours) | 30.0 | 45.4 | 46.6 | 40.6 |
| ε-Hybrid (Ours) | 32.5 | 50.2 | 41.2 | 37.8 |
Efficiency via Attention Masks
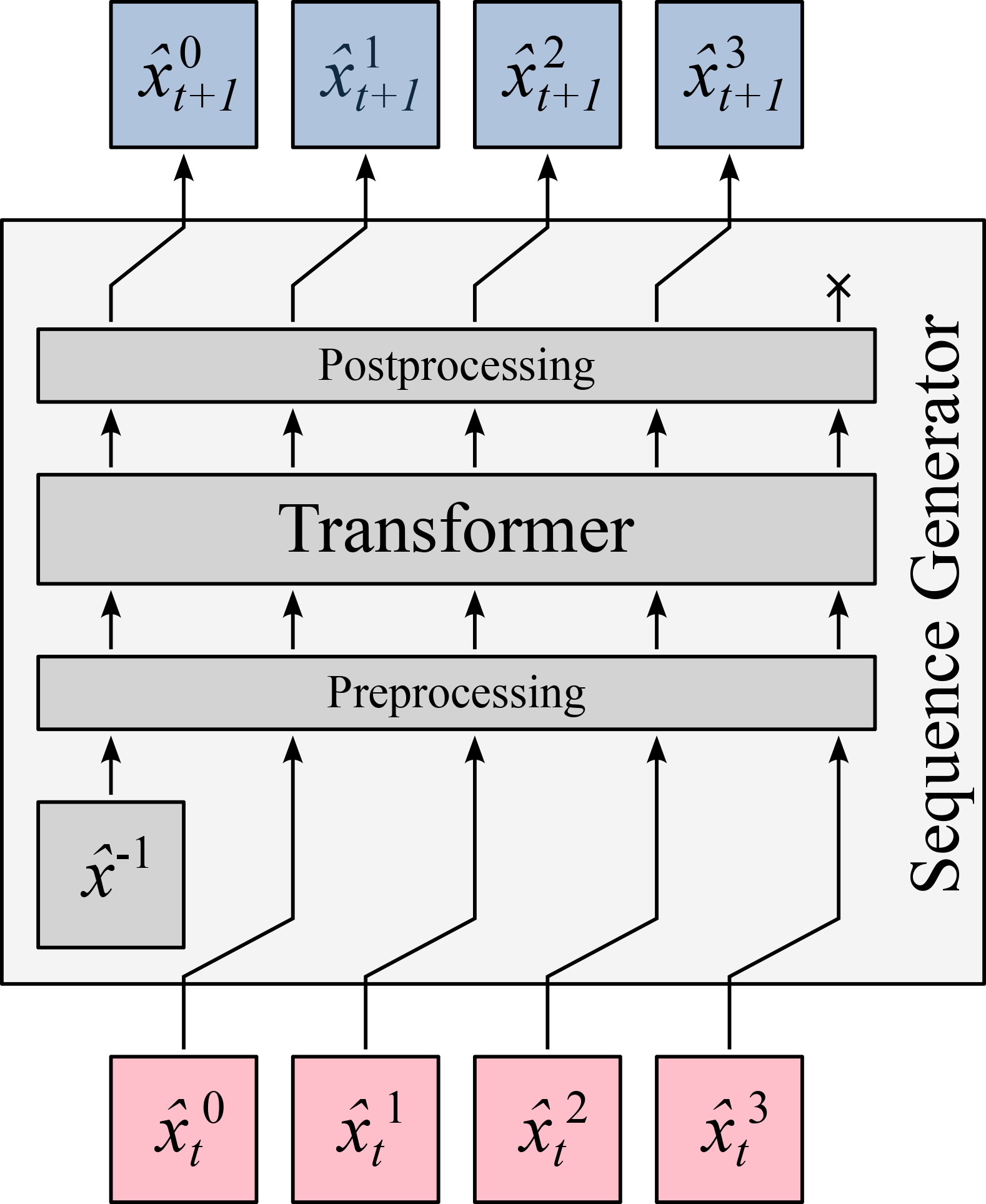
An integral part of our framework is optimizing computational efficiency through advanced attention mechanisms. Our attention design leverages:
- KV-Caching: Reuse of finalized (settled) tokens to minimize redundant computations [6].
- Active vs. Settled Tokens: Dynamic partitioning of tokens into:
- Settled Tokens: Finalized outputs eligible for caching.
- Active Tokens: Tokens under current update.
- Worthless Tokens: Tokens yet to be generated or irrelevant to the current context.
This design supports two distinct inference modes:
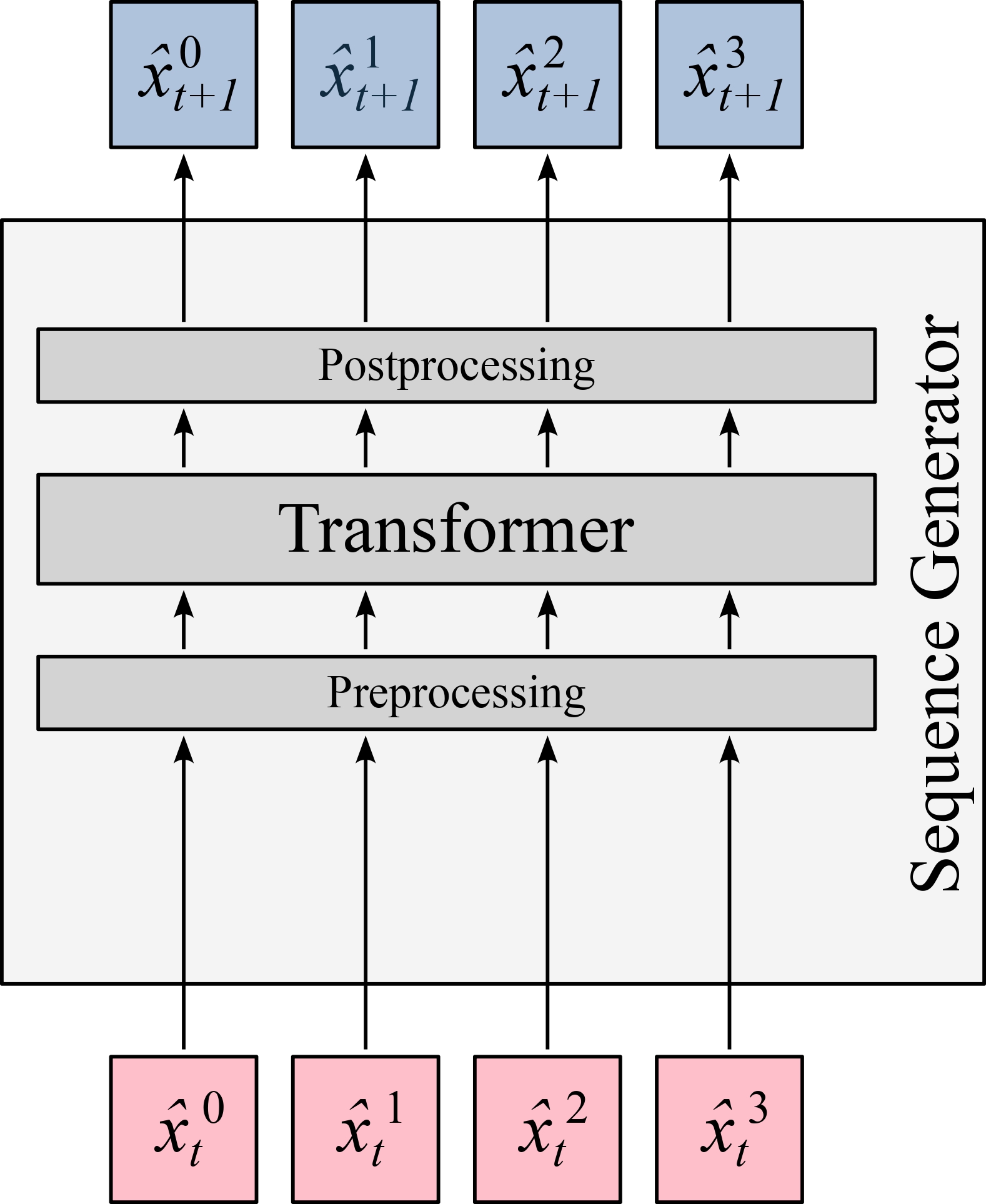
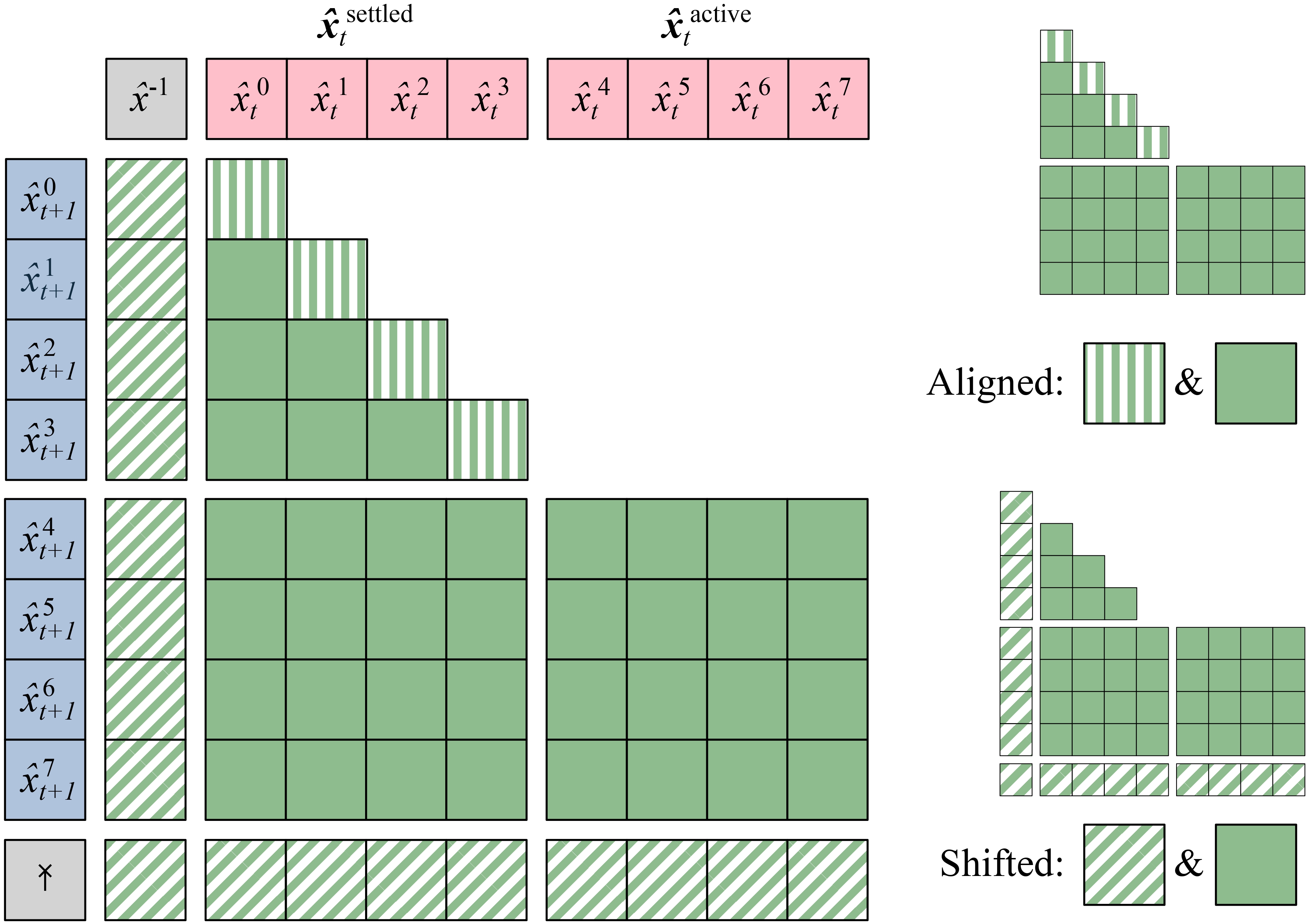
- Aligned (Masked Language Model Style): (See Figure 4)
- Shifted (Autoregressive Style): (See Figure 5)
Additionally, Figure 6 demonstrates the training attention mask that effectively partitions tokens, contributing to significant improvements in efficiency.
Conclusion and Future Work
By unifying the autoregressive and diffusion paradigms through hyperschedules, hybrid noising, and our Adaptive Correction Sampler (ACS), we demonstrate significant improvements in both sequence fluency and computational efficiency. Our flexible approach supports diverse inference strategies—from masked token predictions to autoregressive generation—paving the way for novel applications and further research.
Future Research Directions:
- Investigating more nuanced hyperschedule designs for finer-grained control.
- Adapting the hybrid noising strategy to new domains such as code generation.
- Conducting extensive studies on the trade-offs between quality and efficiency in real-world applications.
For further details, please refer to our full paper on arXiv.
Stay tuned for more updates as we continue to push the boundaries of sequence generation!
Table of Figures
| Figure No. | Title | Description |
|---|---|---|
| 1 | Hyperschedules | Shows various hyperschedule designs that customize noise levels per token. |
| 2 | Hybrid Noising | Depicts the hybrid noising process integrating token masking and random perturbations [3,4]. |
| 3 | Quality-Diversity Trade-offs | Compares perplexity and MAUVE scores to demonstrate improved quality-diversity trade-offs [3,4]. |
| 4 | Transformer (Aligned) | Visualizes the aligned attention mask configuration that leverages KV-caching [6]. |
| 5 | Transformer (Shifted) | Shows the shifted attention configuration suited for autoregressive generation [6]. |
| 6 | Training Attention Mask | Demonstrates token partitioning during training into settled, active, and worthless tokens [6]. |
References
- Radford, A., et al. (2019). Language Models are Unsupervised Multitask Learners. OpenAI.
- Ho, J., Jain, A., & Abbeel, P. (2020). Denoising Diffusion Probabilistic Models. Advances in Neural Information Processing Systems.
- Lou, et al. Discrete Diffusion Modeling by Estimating the Ratios of the Data Distribution International Conference on Machine Learning.
- Sahoo, et al. Simple and Effective Masked Diffusion Language Models. Conference on Neural Information Processing Systems.
- Arriola, et al. Block Diffusion: Interpolating Between Autoregressive and Diffusion Language Models International Conference on Learning Representations.
- Vaswani, A., et al. (2017). Attention Is All You Need. Advances in Neural Information Processing Systems.